前回と同様の手順で下図のように塗り分けられたデータを分類してみました。

ですよねぇ。
青点が両側に分離されてしまってますから、緑や赤との境界が決まりません。
「全部、青」と言われれば「そうなのかなぁ」といったところです。
このようなデータでも「隠れ層(中間層)」と呼ばれる未知数を追加するだけで分類が可能となります。
num_units = 2
x=tf.placeholder(tf.float32,[None,1])
w1=tf.Variable(tf.truncated_normal([1,num_units]))
b1=tf.Variable(tf.zeros([num_units]))
hidden1=tf.nn.relu(tf.matmul(x,w1)+b1)
w0=tf.Variable(tf.zeros([num_units,3]))
b0=tf.Variable(tf.zeros([3]))
f=tf.matmul(hidden1,w0)+b0
p=tf.nn.softmax(f)
t=tf.placeholder(tf.float32,[None,3])
loss=-tf.reduce_sum(t*tf.log(tf.clip_by_value(p,1e-10,1.0)))
train_step=tf.train.AdamOptimizer().minimize(loss)
赤で示した未知数w1、b1とプレースホルダーxから算出されるhidden1というのが隠れ層(中間層)と呼ばれるものです。前回出てきた一次関数f(w0,b0)の計算からソフトマックス関数の適用までと、瓜二つの繰り返しのように見えます。
このトレーニングを十分に繰り返したあとのhidden1の値の分布を示します。

num_units=2としているので、hidden1は2次元となっています。横軸はhidden1[ 0 ]、縦軸はhidden1[ 1 ]です。
-5<=x<=5で50分割したものを入力して計算したhidden1の値を打点しました。x=-5はhidden1=(0,0)に変換されるようです。逆にx=+5はhidden1=(15,25)に変換されます。
すなわち、この中間層はX軸を2次元上の曲線(あるいは2つの線分)に変換していたのです。
こうなってしまえば、正負で分離されていたと思われた青点も平面上の一つの直線の同じ側として一括りに扱うことが可能となります。
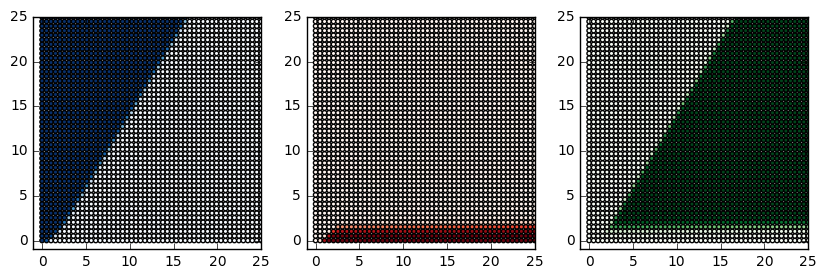
そうなるように適切にw0とb0を求めて、青赤緑それぞれの確率を計算して描画します。

隠れ層(中間層)を使用することで、複雑な領域分けが可能となりました。
# coding: utf-8
# In[ ]:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import multivariate_normal, permutation
import pandas as pd
from pandas import DataFrame, Series
np.random.seed(20170426)
# In[ ]:
num_train=300
x=np.random.rand(num_train)*10-5
t=np.zeros( (num_train,3) )
df=DataFrame(np.c_[x,t],columns=['x','blue','red','green'])
for i in range(num_train):
if df.x[i]<-2.25:
df.blue[i]=1
elif df.x[i]>2.25:
df.blue[i]=1
elif df.x[i]<0:
df.red[i]=1
else:
df.green[i]=1
#データフレームから行列変換します。train_tはOne-Hot表現にしています。
train_x=df['x'].as_matrix().reshape([len(df),1])
train_t=df[ ['blue','red','green'] ].as_matrix().reshape([len(df),3])
# In[ ]:
fig = plt.figure(figsize=(3,3))
subplot = fig.add_subplot(1,1,1)
subplot.set_xlim([-5,5])
subplot.set_ylim([-1,1.5])
red=df[df.red==1]
subplot.scatter(red.x,-0.5*red.red+0.05, color='r', marker='o')
blue=df[df.blue==1]
subplot.scatter(blue.x,-0.5*blue.blue-0.05, color='b', marker='o')
green=df[df.green==1]
subplot.scatter(green.x,-0.5*green.green, color='g', marker='o')
# In[ ]:
num_units = 2
x=tf.placeholder(tf.float32,[None,1])
w1=tf.Variable(tf.truncated_normal([1,num_units]))
b1=tf.Variable(tf.zeros([num_units]))
hidden1=tf.nn.relu(tf.matmul(x,w1)+b1)
w0=tf.Variable(tf.zeros([num_units,3]))
b0=tf.Variable(tf.zeros([3]))
f=tf.matmul(hidden1,w0)+b0
p=tf.nn.softmax(f)
t=tf.placeholder(tf.float32,[None,3])
loss=-tf.reduce_sum(t*tf.log(tf.clip_by_value(p,1e-10,1.0)))
train_step=tf.train.AdamOptimizer().minimize(loss)
# In[ ]:
sess=tf.Session()
sess.run(tf.initialize_all_variables())
# In[ ]:
i=0
#10000回トレーニングを実施します。
for _ in range(10000):
i += 1
sess.run(train_step,feed_dict={x:train_x, t:train_t})
if i%1000==0:
loss_var=sess.run(loss,feed_dict={x:train_x, t:train_t})
print '%d:loss=%f' % (i,loss_var)
# In[ ]:
# 2ノードの隠れ層(中間層)で表現される仮想平面を描画します。
test_x=np.linspace(-5,5,50).reshape([50,1])
h_val=sess.run(hidden1,feed_dict={x:test_x})
plain=DataFrame(np.c_[test_x,h_val],columns=['x','x1','x2'])
p_val=sess.run(p,feed_dict={hidden1:h_val})
line=DataFrame(np.c_[h_val,p_val],columns=['x1','x2','blue','red','green'])
fig = plt.figure(figsize=(10,3))
subplot = fig.add_subplot(1,3,1)
subplot.set_xlim([-1,25])
subplot.set_ylim([-1,25])
subplot.scatter(line.x1,line.x2, s=10, c=line.blue, cmap='Blues')
subplot = fig.add_subplot(1,3,2)
subplot.set_xlim([-1,25])
subplot.set_ylim([-1,25])
subplot.scatter(line.x1,line.x2, s=10, c=line.red, cmap='Reds')
subplot = fig.add_subplot(1,3,3)
subplot.set_xlim([-1,25])
subplot.set_ylim([-1,25])
subplot.scatter(line.x1,line.x2, s=10, c=line.green, cmap='Greens')
# In[ ]:
# 仮想平面と青赤緑の関係です。
plane=[]
for x2 in np.linspace(0,25,50):
for x1 in np.linspace(0,25,50):
plane.append( (x1,x2) )
p_val=sess.run(p,feed_dict={hidden1:plane})
image=DataFrame(np.c_[plane,p_val],columns=['x1','x2','blue','red','green'])
fig = plt.figure(figsize=(10,3))
subplot = fig.add_subplot(1,3,1)
subplot.set_xlim([-1,25])
subplot.set_ylim([-1,25])
subplot.scatter(image.x1,image.x2, s=10, c=image.blue, cmap='Blues')
subplot = fig.add_subplot(1,3,2)
subplot.set_xlim([-1,25])
subplot.set_ylim([-1,25])
subplot.scatter(image.x1,image.x2, s=10, c=image.red, cmap='Reds')
subplot = fig.add_subplot(1,3,3)
subplot.set_xlim([-1,25])
subplot.set_ylim([-1,25])
subplot.scatter(image.x1,image.x2, s=10, c=image.green, cmap='Greens')
# In[ ]:
# テストデータとして-5から5を50分割したtest_xを作成します
# このテストデータで、青赤緑それぞれの確率を計算して描画します
test_x=np.linspace(-5,5,50).reshape([50,1])
p_val=sess.run(p,feed_dict={x:test_x})
line=DataFrame(np.c_[test_x,p_val],columns=['x','blue','red','green'])
fig = plt.figure(figsize=(3,3))
subplot = fig.add_subplot(1,1,1)
subplot.set_xlim([-5,5])
subplot.set_ylim([-1,1.5])
subplot.plot(line.x,line.blue,color='b')
subplot.plot(line.x,line.red,color='r')
subplot.plot(line.x,line.green,color='g')
red=df[df.red==1]
subplot.scatter(red.x,-0.5*red.red+0.05, color='r', marker='o')
blue=df[df.blue==1]
subplot.scatter(blue.x,-0.5*blue.blue-0.05, color='b', marker='o')
green=df[df.green==1]
subplot.scatter(green.x,-0.5*green.green, color='g', marker='o')